Fale stojące jako nośnik przekazu informacji

Fale stojące nie przekazują energii, a jedynie pompują energię w przód i w tył w połowie długości fali. Połowa długości fali zupełnie wystarcza nawet do łączności międzyplanetarnej, jeśli mamy do czynienia z falami stojącymi w przestrzeni logarytmicznej.

Długości fal stojących gęstości w przestrzeni logarytmicznej wynoszą 2 × 3k, to znaczy 6, 18, 54, 162 i 486 jednostek logarytmu naturalnego. Stąd połowy długości odpowiadają 3, 9, 27, 81 i 243 jednostkom, zaś względne wielkości/skale 1,3 3,9 11,7 35,2 i 105,5 odpowiadają tym samym rzędom wielkości.

Węzły występują dokładnie w tych samych interwałach, stąd punkty węzłów oznaczających wielkości/skale przyjmują wartości 1:20, 1:8103, 1:5,32 ×10¹¹, 1:1,5×10³⁵ i 1:3,4×10¹⁰⁵. W ramach zakreślonych przez te wielkości/skale możliwa jest łączność między dwoma punktami węzłowymi.

Możliwość modulowania fali stojącej jest ograniczona do jej punktów węzłowych, ponieważ tylko w bezpośredniej bliskości tych punktów można dostarczać do fali energię lub odprowadzać ją z niej. Jeśli jest to fala stojąca w przestrzeni liniowej, punkty węzłowe stanowią po prostu miejsca, w których możliwe jest dołączenie zewnętrznego procesu oscylacyjnego.

Natomiast punkty węzłowe fali stojącej w przestrzeni logarytmicznej stanowią szczególne wielkości/skale posiadające różne przypisane im częstotliwości. Aby obliczyć te częstotliwości, konieczna jest znajomość matematycznych podstaw Ogólnej Teorii Skal.

 

Fizyka osi liczbowej

Świat wielkości jest niczym innym jak ciągiem liczb logarytmicznych znanych matematyce od czasów Napiera (1600). To, co jest w tym jednak nowe, to podstawowa wiedza mówiąca, że oś liczbowa posiada strukturę harmoniczną, która sama w sobie stanowi przyczynę fali stojącej ciśnienia.

Już Leonard Euler (1748) wykazał, że liczby niewymierne i przestępne można przedstawić w postaci ciągu ułamków, których wszystkie elementy (dzielne i dzielniki) są liczbami naturalnymi. W roku 1928 Khintchine dostarczył na to ogólnego dowodu.

W teorii liczb oznacza to, że wszystkie liczby można zbudować z liczb naturalnych, a ogólną zasadą ich budowy jest ciąg ułamków. Z kolei wszystkie liczby naturalne 1, 2, 3, 4, 5... są zbudowane z liczb pierwszych, to znaczy takich liczb naturalnych, których nie można dzielić dalej bez reszty, takich jak 1, 2, 3, 5, 7, 11, 13, 19, 23, 29, 31... (1 tradycyjnie nie jest zaliczane do liczb pierwszych, aczkolwiek spełnia wszystkie kryteria tych liczb). Rozkład liczb pierwszych na osi liczbowej jest tak nieregularny, że nie udało się znaleźć wzoru, który dokładnie określałby ich rozkład – uczyniła to dopiero Ogólna Teoria Skal.

Rozkład liczb jest rzeczywiście bardzo nieregularny, ale jedynie na liniowej osi liczbowej. Na logarytmicznej osi liczbowej duże dziury między liczbami pierwszymi powtarzają się w regularnych odstępach. Zauważył to już Gauss (1795). Tak więc zestaw pi(n) liczb pierwszych można określić w przybliżeniu aż do n prostym wzorem pi(n) = n / ln n.

Powodem występowania tego zjawiska jest istnienie na logarytmicznej osi liczbowej stojącej fali gęstości, której węzły przyciągają liczby. Tam właśnie będą się „kumulować” liczby pierwsze i tworzyć liczby złożone, czyli niepierwsze, takie jak siedem liczb niepierwszych od 401 do 409. Stąd „dziura liczb pierwszych” wystąpi w tym miejscu.

Dokładnie tam, gdzie liczby niepierwsze (to znaczy skupienia liczb pierwszych) wystąpią na logarytmicznej osi liczbowej, tam materia koncentruje się na logarytmicznej osi pomiarów. To nie ma nic wspólnego z magią. Jest to, po prostu, konsekwencja faktu, że wielkości/skale są logarytmiczne, to znaczy są liczbami.

Tak więc oś wielkości logarytmicznych nie jest niczym innym jak osią liczb logarytmicznych, a ponieważ stojąca fala ciśnienia jest własnością osi liczb logarytmicznych, określa ona częstotliwość rozkładu materii na wszystkich fizycznie kalibrowanych osiach logarytmicznych – osi stosunków rozmiarów, mas, częstotliwości, temperatur, prędkości etc.

Aby znaleźć punkt węzłowy na osi logarytmicznej, potrzebna jest tylko oś liczbowa (którą każdy zna) oraz naturalna standardowa miara, przy pomocy której należy skalibrować oś liczbową. Długość stojącej fali gęstości na logarytmicznej osi liczbowej jest znana. Odległość między sąsiednimi węzłami wynosi trzy jednostki naturalnego logarytmu. Stąd łatwo obliczyć wszystkie węzłowe wartości Xn przy użyciu prostego wzoru Xn = Y × exp(n), gdzie Y jest naturalną standardową miarą, n = 0, ±3, ±6, ±9...

Wartości częstotliwości węzłów wynoszą na przykład 5Hz (n = –54), 101Hz (n = –51), 2032 Hz (n = –48), 40,8 kHz (n = –45), 820 kHz (n = –42), 16,5MHz (n = –39), 330,6MHz (n = –36) etc., zaś zakresy częstotliwości wynoszące około 5 Hz, 100 Hz, 2 kHz etc. są predestynowane do transmitowania energii w ośrodku skończonym.

Tam również, w logarytmicznej przestrzeni, mieszczą się częstotliwości fali nośnej. Częstotliwości występujące w pobliżu punktu węzłowego nie są zbyt pospolite w przyrodzie, ale są stosowane w technice.

 

Naturalne standardowe miary – klucz do ogólnego skalowania

Dokładna wiedza o harmonicznej strukturze przestrzeni logarytmicznej stanowi wrota do ogólnego skalowania. Aby otworzyć te wrota, potrzebny jest klucz – naturalne standardowe miary (patrz poniższa tabela).

 

 

 

 

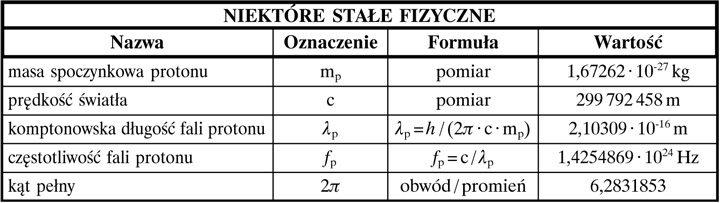
Naturalne standardowe miary są faktycznie wartościami punktów węzłowych. W punkcie węzłowym fali stojącej nie występują drgania, panuje tam bezruch. Z tego względu naturalne standardowe miary mają dużą stabilność. Masa spoczynkowa protonu pozostaje stała przez okres minimum 10³⁰ lat. Z tego samego również powodu prędkość światła w próżni stanowi raczej stałą wartość. Istnienie stałych miar stanowi fizyczną podstawę naturalnej metrologii, na której opiera się Ogólna Teoria Skal.

 

Ciąg ułamków jako „Formuła Świata”

W roku 1950 Gantmacher i Kerin udowodnili, że przestrzenny rozkład swobodnie poruszających się cząstek w liniowych łańcuchach oscylujących można opisać przy pomocy ciągów ułamkowych.

Terskich (1955) udowodnił to samo dla nieliniowych układów łańcuchowych. W roku 1982 wykazałem, że rozkład materii w przestrzeni logarytmicznej również posiada strukturę ciągów ułamkowych. Struktura ta mówi, że koncentracja materii rośnie hiperbolicznie w bliskości punktów węzłowych.

W pierwszym przybliżeniu rozkład materii w przestrzeni logarytmicznych wielkości ma fraktalowy wymiar pyłu Cantora, ale jest deformowany hiperbolicznie w bliskości punktów węzłowych (patrz poniższe ilustracje).

 

 

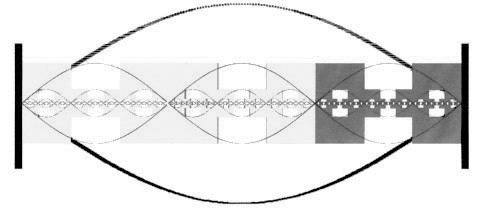
Rozkład materii w logarytmicznej przestrzeni wielkości w pierwszym przybliżeniu posiada fraktalowy wymiar pyłu Cantora, ale jest deformowany hiperbolicznie w pobliżu węzła.