Konwencja w matematyce nakazuje dzielić liczby naturalne na dwie grupy: liczby pierwsze i liczby złożone.
Liczba pierwsza to taka, która dzieli się wyłącznie przez siebie oraz przez 1.
Za liczbę złożoną uznaje się liczbę, która ma więcej niż 2 dzielniki. Jak wykażę, nie jest to wcale wyczerpująca odpowiedź. Co więcej, ten błąd ma fundamentalne znaczenie w naszej niewłaściwej interpretacji rzeczywistości. Liczby pierwsze wcale nie są rozmieszczone chaotycznie bądź przypadkowo. Po prostu, nie zrozumieliśmy systemu liczb.
Pierwszą rzeczą, jaką zrobiłem, było zastosowanie Mod 9 do pierwszych 65 000 liczb pierwszych, w wyniku czego odkryłem ku mojemu zaskoczeniu, że jako wyniki otrzymałem 1, 2, 4, 5, 7 lub 8 dla wszystkich liczb pierwszych większych lub równych pięć. Innymi słowy, te liczby pierwsze były wyłącznie złożone z grup rodzin numerów 1, 4, 7 oraz 2, 5, 8.
Gdy przeanalizowałem naturalną skalę muzycznych interwałów, odkryłem 72-liczbową sekwencję (modulus) składającą się z sześciu oktaw po 12 nut. Po wielu rozważaniach ułożyłem liczby od 1 do 72 w sześć kolumn, jak pokazuje to tabela na następnej stronie. Następnie zaznaczyłem liczby pierwsze na czerwono i zastosowałem Mod 9, jak to pokazuje prawa strona tabeli.
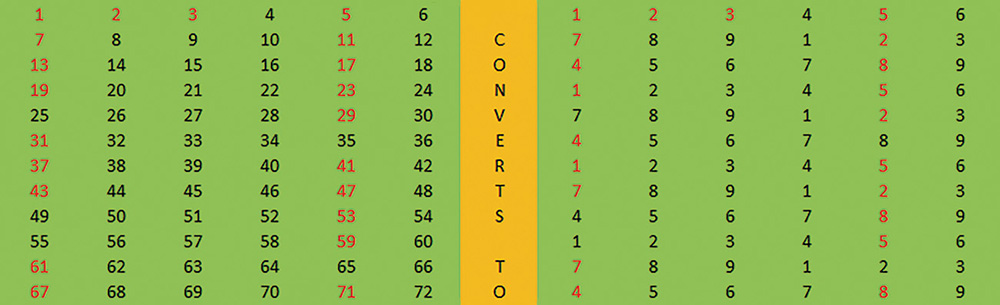
Liczby pierwsze występują wyłącznie w kolumnie 1 i w kolumnie 5, w których Mod 9 po prostu powtarza odpowiednio 7, 4, 1 oraz 5, 2, 8. Liczby pierwsze będą dawać wyłącznie te wartości reszty w nieskończoność.
Usuwając kolumny 2, 3, 4 oraz 6, zostaną tylko kolumny 1 oraz 5, które zawierają same liczby pierwsze (zaznaczone na czerwono) i inne, „pozostałe” liczby (zaznaczone na czarno).
Te „pozostałe” liczby można od razu określić jako wytwory liczb pierwszych, np. 5 × 7 = 35, 5 × 11 = 55, 5 × 13 = 65 itd. lub potęgi (wykładniki) liczby pierwszych, np. 52 = 25, 72 = 49, itd.
Te „pozostałe” liczby są obecnie klasyfikowane jako liczby złożone, jednak jak zobaczymy, powinny zostać przeklasyfikowane na „liczby pierwsze złożone”. Powinno się o nich myśleć jak o części systemu liczb pierwszych, a nie systemu liczb złożonych, tak jak do tej pory.
Liczby, o których mowa, są tworzone wyłącznie przez kombinacje liczb pierwszych zaczynających się od 5. Są po prostu samopodobnymi, fraktalnymi powtórzeniami sekwencji liczby pierwszej i wszystkich jej możliwych kombinacji.
Warto powiedzieć, chociaż wykracza to poza zakres niniejszego artykułu, że kombinacja liczb pierwszych oraz liczb pierwszych złożonych pozwala na istnienie oraz odpowiada za nieskończoną złożoność fizycznej rzeczywistości. Rzeczywistość jest tworzona przez nieskończoną, fraktalną ekspansję liczb pierwszych, które tworzą siatkę – przypomina to pająka przędzącego sieć…
Dowód wizualny
Jeśli utworzymy kwadratową spiralę liczb i zaznaczymy w niej liczby tradycyjnie uznawane za pierwsze, to otrzymamy coś, co nazywane jest spiralą Ulama, w której liczby pierwsze pojawiają się głównie na niektórych przekątnych.
Jeśli dodamy liczby pierwsze złożone i wykładniki, to zaobserwujemy coś bardziej określonego – obraz niezwykłej koherencji i kongruencji.
Dowody numeryczne
Aby wzmocnić moją argumentację dotyczącą liczb pierwszych, jak również by pokazać, że Mod 9 jest przydatny do wyłuskania informacji niemożliwych do uzyskania w inny sposób, musimy spojrzeć na drugi aspekt problemu i zbadać liczby „niepierwsze”, które znamy jako złożone. Każda z tych liczb ma wiele dzielników oprócz siebie samej i 1. W analizie poświęconej liczbom złożonym sekwencja Mod 9 wygląda następująco:
2 3 4 6 8 0 1 3 5 6 7 0
2 3 4 6 7 8 0 1 3 5 6 7 8 0
2 3 4 6 8 0 1 3 4 5 6 7 0 1
2 3 4 6 8 0 1 2 3 5 6 7 0
2 3 4 5 6 8 0 1 3 4 5 6 7
Czy widzicie, że te liczby próbują się zorganizować, ale nie do końca im to wychodzi? Gdy wyłączymy liczby pierwsze złożone oraz wykładniki z tej złożonej sekwencji, wszystko staje się jasne! Tam, gdzie wcześniej nie było kongruencji (zbieżności), teraz już jest – 12-cyfrowa powtarzająca się sekwencja, która wygląda następująco:
2 3 4 6 8 0 1 3 5 6 7 0

Spirala Ulama (http://en.wikipedia.org/wiki/Ulam_spiral)
Można ją rozbić na trzy czteroliczbowe segmenty, aby zilustrować coś, co nazywam trójwymiarową „symetrią liczbową”, która podkreśla grupy rodzin liczb w utworzonych kolumnach:
2 3 4 6
8 0 1 3
5 6 7 0